Pythagoras in Gizeh?

Fig. 1 - Satz des Pythagoras

Der Satz von Pythagoras ist das zweite große geometrische Zahlengeheimnis welches in Ägypten, und ganz speziell in den Giza-Pyramiden "entdeckt" wird. Ob nun Pi oder Pythagoras häufiger strapaziert wird weiß ich nicht, aber zu Pythagoras sind letzthin modernere Arbeiten erscheinen, eine davon bespreche ich auf der nächsten Seite.
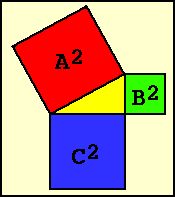
Genau wie Pi ist der "Satz des Pythagoras" eigentlich nichts besonderes, obwohl die nebenstehende Grafik, die diesen Satz verdeutlicht, auf den Laien einen geheimnisvollen Eindruck erwecken mag.
Pythagoras, der griechische Philosoph und Mathematiker (ca. 570-480 v. Chr.), gründete eine Schule der Philosophie, in der Musik und mit ihr Zahlen eine besondere Bedeutung besaßen. Die gesamte Welt sollte sich aus dem Zusammenwirken von Zahlen erklären lassen, als Konsequenz daraus suchten die Pythagoräer nach mathematischen Gesetzmäßigkeiten zur Erklärung der Natur.
Eine der Gesätzmäßigkeiten die dabei gefunden wurde betraf sogenannte rechtwinklige Dreiecke. Das sind Dreiecke in ein Winkel 90, ein "rechter Winkel" eben, auftaucht. Die Seiten die an den Rechten Winkel grenzen nennt man Katheten, die Seite die die beiden Katheten verbindet wird Hypotenuse genannt. Die Pythagoräer fanden nun heraus:

Die Hypotenuse ist immer die längste Seite
Ein Quadrat, welches mit der Hypotenuse konstruiert wird, besitzt immer dieselbe Fläche wie die beiden Quadrate, die man mit den Kathetenlängen konstruieren kann zusammengenommen.

Mathematisch wird die Zeichnung daher wie folgt beschrieben: A² = B² + C² . Und dies soll sich in Gizeh finden lassen! Schaun wir mal...

Erich von Däniken schreibt in Rätsel (6): "Die drei Pyramiden von Gizeh sind untereinander im pythagoreischen Dreieck ausgerichtet, deren Seiten stehen im Verhältnis 3:4:5". Dies ist bei genauerer Betrachtung allerdings höchst fraglich...

Fig. 2 - Giza-Dreieck

Um festzustellen, daß die drei Gizamiden nicht in einem pythagoreischen Dreieck angeordnet sein können reicht ein einziger Blick auf eine Karte des Giza-Plateaus (wenn man weiß, was ein pythagoreisches Dreieck ist, natürlich :-) ). Alle drei Pyramiden stehen fast auf einer Linie (im Orion-Teil betrachte ich diese "Giza-Diagonale" genauer), nur die Spitze der Mykerinos-Pyramide weicht leicht nach Osten ab. Kein rechtwinkliges (pythagoreisches) Dreieck weit und breit. Die Behauptung Dänikens ist einfach Mist, ein deutlicher Beleg dafür, daß der "große Meister" offenbar keine Ahnung hat worüber er überhaupt schreibt.

Das "Verhältnis von 3:4:5" taucht allerdings auch in Büchern von Autoren auf, die etwas mehr Ahnung haben worüber sie schreiben. So taucht diese Behauptung bereits beim schon erwähnten Piazzi Smyth im Jahre 1864 auf. Dieses Verhältnis bezieht sich allerdings nicht, wie Däniken fälschlicherweise interpretierte, auf die Pyramidenanordnung, sondern auf die Pyramidengrundseiten!!!
Wenn die Pyramiden im 3:4:5-Verhältnis stehen, muss also ein gemeinsames Längenmaß vorhanden sein, welches dreimal in der kleinsten, der Mykerinospyramide, viermal in der zweitgrößten Chephrenpyramide, und fünfmal in der größten, der Cheopspyramide, vorkommt.

Dies kann man wieder einmal schnell mit einem simplen Taschenrechner prüfen. Suchen wir zunächst das "Grundmaß":

Pyramide	Basisbreite	Faktor	Breite/Faktor
Cheops	230,36 m	5	46,07 m
Chephren	215,50 m	4	53,87 m
Mykerinos	108,50 m	3	36,16 m

Tab. Pyt 1 - Die "Basiseinheiten" der Pyramiden

Hm, nicht sehr überzeugend. Die "Basiseinheit" schwankt zwischen 36 und 53 Metern, um knapp 67%, das ist kein "Fehler" mehr. Bei einem 3:4:5-Verhältnis müßten die Pyramiden mit den verschiedenen "Grundmaßen" folgende Größen besitzen:

Basis	Cheops	Fehler	Chephren	Fehler	Mykerinos	Fehler
Cheops	230,36	0 m	184,28 m	-31,22 m	138,21 m	+29,71 m
Chephren	269,35 m	+38,99 m	215,50 m	0 m	161,61 m	53,11 m
Mykerinos	180,80 m	49,56 m	144,64 m	-70,86 m	108,50 m	0 m

Tab. Pyt 2 - Pyramidengrößen mit den 3 "Basiseinheiten"

Tja, Pech, keine gemeinsame Basisgröße - und daher stehen die Pyramiden auf keinen Fall im 3:4:5-Verhältnis zueinander.

Bliebe noch ein Ausweg, eine Ehrenrettung sozusagen. Nämlich daß die Flächeninhalte der Mykerinos- und Chefrenpyramide zusammen den Flächeninhalt der Cheopspyramide ergeben, unabhängig vom 3:4:5-Verhältnis. Auch dies ist in wenigen Sekunden mit den obigen Daten und einem Taschenrechner überprüfbar: Cheops: 53075 Quadratmeter, Chefren 46440 und Mykerinos 11772 Quadratmeter. Chefren und Mykerinos zusammen ergeben 58212 Quadratmeter - 5137 Quadratmeter größer als Cheops. Dieser "Rundungsfehler" wäre die Basisfläche einer Pyramide mit 71 m Seitenlänge! Nein, die Behauptung ist wieder einmal schlicht falsch.

Nach diesem erneuten Däniken-Fiasko steht's nur noch 9:10 gegen die Pyramidengeheimnisse!

Das heilige Dreieck

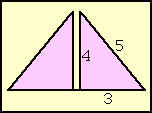
Es gibt allerdings wirklich ein 3:4:5-Dreieck in Giza - eingebaut in die Chephrenpyramide! dieses Dreieck wird "heiliges Dreieck" genannt und von einigen Autoren ebenfalls zum Geheimnis hochstilisiert. Warum?

Normalerweise stehen die Seiten rechtwinkliger Dreiecke in einem ungeraden Verhältnis zueinander, es sind ja letztendlich Quadratwurzeln. Mit diesen konnten die Ägypter nicht umgehen, allerdings waren sie auf gerade diese Dreiecke angewiesen, weil es nur mit ihnen möglich ist, das Land nach jeder Nilüberschwemmung neu aufzuteilen oder die zur Steuererhebung zu ermittelnde Landfläche eines Bauern zu vermessen. Daher konnten sie nur Dreiecke verwenden, bei denen die Quadratwurzeln der Kathetenquadrate ganze Zahlen (1, 2, 3...) ergaben. Das kleinste dieser Dreiecke besitzt eben das Verhältnis 3:4:5 (3² + 4² = 25 = 5²)!
Nimmt man ein Seil mit (3+4+5) Knoten, fixiert den 5. Knoten im Boden, geht mit der längeren Seite 4 Knoten weit in die gewünschte Richtung, fixiert diesen Knoten dort ebenfalls, und bringt die beiden losen Enden straff zusammen, erhält man automatisch einen rechten Winkel, und kann einfach ein Rechteck konstruieren. Etliche Kammern in den Pyramiden sind eindeutig mit dieser Methode konstruiert worden!
Um so ein Dreieck konstruieren zu können - braucht man da nicht nur den Satz von Pythagoras UND Wissen über Quadratwurzeln? Also DOCH ein Zeichen für Astronauten?

Nicht notwendig, denn wie ich in einem Experiment herausfand, findet man dieses Verhältnis ganz fix selbst heraus - ohne die zugrundeliegende Theorie zu kennen! Dazu braucht man nur ein Seil mit vielen Knoten (in gleichen Abständen, selbstverständlich) und drei Helfer. Einer stellt sich an einen Eckpunkt und hält einen Knoten in der Mitte fest. Zwei gehen jeweils in ganzen Knotenschritten in die zu vermessenden Richtung, während der Meistervermesser (in dem Falle ich ;-) ) in der Mitte zwischen den beiden Läufern versucht, die beiden Seilenden so zusammenzubringen, daß Knoten über Knoten liegt. Der Eckmann peilt, ob es ungefähr ein rechter Winkel ist, und schwupps hat man sein magisches Dreieck. Die Ägypter waren nicht dumm, und irgendwann wird ihnen sicherlich aufgefallen sein, daß man immer nur ganz bestimmte Knotenverhältnisse pro Seite erhielt - und damit zwei Leute wegrationalisierte, weil man jetzt die Vermessung planen konnte. Dafür braucht man weder Götter noch Astronauten.

Fig. 3 - Pyramidenschnitt

Allerdings besteht schon ein kleiner Unterschied zwischen dem Ausmessen eines Ackers und der Verankerung eines heiligen Dreiecks in der zweitgrößten Pyramide der Welt! Sägt man nämlich die Chefrenpyramide in ihrer Mitte durch - bitte, Kinder, macht das nicht zu Hause - sieht man, daß jedes Viertel exakt im 3:4:5-Verhältnis errichtet wurde! Also doch!
Trotzdem ist das nichts besonderes (auch wenn es Sie inzwischen anödet, das zu hören), die ägyptischen Baumeister hatten nämlich überhaupt keine Chance, an dem heiligen Dreieck vorbeizubauen! Zumindest nicht in allen Pyramiden, die im 1:21-Verhältnis gebaut wurden. Sie erinnern Sich? Steigungen? Elle-Finger-Verhältnisse? Die Chefrenpyramide ist im 1:21-Verhältnis gebaut, also eine Elle Höhe auf 21 Finger Länge. Die Höhe ist demnach ein ganzzahliges Vielfaches einer Elle, die Breite ein ganzzahliges Vielfaches von 21 Fingern. Eine Elle besteht aber aus 28 Fingern, das echte Bauverhältnis war demnach 21:28. Kürzt man eine 7 heraus, bleibt ein Höhen-Breitenverhältnis von 3:4! Dies sind die beiden Katheten eines rechtwinkligen Dreiecks, die dritte Seite muss daher 5 Längeneinheiten betragen. Bei allen 1:21-Pyramiden. Auch dies ist daher keinerlei Beweis dafür, daß die Ägypter irgend etwas von höherer Geometrie verstanden.