Another numerological mystery in some of the pyramids is the famous axiom of Pythagoras. Discovered in the 6th century B.C. it should be a sign for Gods or astronauts, too, if found in old kingdom Egypt. Some authors claim this to be another sign of early technical cultures, others see it as proof that the pyramids are much younger than thought of. Let's have a look at this mystery, too.
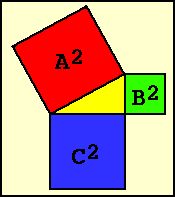Pythagoras axiom deals with a special kind of triangles, the square-angled ones. These triangles have two sides forming a square angle with each other (the kathetes) and a third side connecting them, the hypothenuse. Fascinating: The hypothenuse is always the longest side.
Pythagoras found out, that the combined surface areas of two squares constructed with the kathetes is identical to the area of the square constructed with the hypothenuse.
Or, mathematically, A2 = B2 + C2 . And this construct should be present in the Giza-plateau. Let's have a look!
Erich von Daeniken claims in his book "Eyes of the Sphinx", that the 3 pyramids of Giza are arranged in a squared triangle, and that their sides are in a perfect 3:4:5 ratio to each other. Funny, when I take a look at the three pyramids, I can see no sign of a squared triangle. All three pyramids are standing nearly on a line, only the center of the pyramid of Menkaure deviates a little bit to the east of this line (in fact, the south-east corners of all three pyramids are exactly in line!). Surely, there is no squared triangle in sight, even more no 3:4:5-triangle.
But what about the 3:4:5 proportions of their sides? Well, that is easy to check. The base length of Menkaures pyramid should be 3 length units long, Chefrens 4 and Chufus 5. So lets calculate the base length unit: Menkaure (108.5 m) divided by 3 gives 36,16 m, Chefren 215.50 m/4 = 53,87 m and Chufu 230,38/5 = 46,08 m. Ups, there seems to be no common base unit of this kind used in the three pyramids. And their sides are in no way in a 3:4:5-ratio.
Well, last try. Maybe the surface areas of the pyramid bases are reflecting the axiom of Pythagoras. That means, that the base areas of Menkaures pyramid and of Chephren's pyramid together are as big as the surface area of Chufus pyramid. Well, thats easy to check, with the given numbers and a pocket calculator you get: Chufu 53075 square meters, Chephren 46440 square meters, Menkaure 11772 square meters. Area Menkaure plus area Chephren makes - 58212 square meters! This is 5137 square meters too big, the difference is equivalent to a pyramid with shocking 71 meters base length! This is no minor calculating mistake, its the simple proof that Pythagoras played no role in Egypt or the construction of Giza, too.
But whats the talk about this 3:4:5-triangle? This is called a "holy triangle" and can really be found in Giza! Unfortunately, the sides of most of the squared rectangles have a fractioned ratio to each other, and with such ratios the Egyptians couldn't or didn't work (see Pi). The Egyptians on the other hand NEEDED these triangles to divide the land new after each flooding of the Nile, because it washed away all boundary markers. The only useable triangle for them was one, where she square roots of the squares constructed with each side are in a whole-number-ratio to each other, the smallest one has the sides 3, 4 and 5 units (32 + 42 = 25 = 52)!
If you tie 12 equally spaced knots into a rope, fix the rope at the 5th knot to the ground, go with the longer side 4 knots in one direction, fix the rope there too, and then try to bring both lose ends together, you will automatically get a right angle! And with this you can construct a rectangle.
This method was used in old Egypt, and it was built into Chephren's pyramid. But to construct it, one had to know the very essence of Pythagoras axiom! One had to know about square roots, too. Both things the old Egyptians didn't know. A sign of God or astronauts?
I think this conclusion is not necessary, because the 3:4:5-relation can be found very easily, as I tried in an experiment. You need a long rope with equally spaced knots, 3 helpers and a master measurer (me :-) ). One helper, the "corner man" goes to the corner to measure from and holds a knot in the middle of the rope, two "runners" are going into the directions to be measured, one whole knot each step. And the master measurer in the middle tries to get both ends of the rope together, so that knot lies on knot. The corner man checks if he has a right angle, and voila, you get your holy rectangle in a jiffy. It is not necessary to have any information about Pythagoras or his axiom, no need to know square roots or other elements of geometry. And if the Egyptians were not dumb they found out soon, that there was no corner man necessary if you use specific knot-ratios on each side.
But it is really another task to put this holy triangle into the foundation of a pyramid, isn't it? Again: No. The engineers had in fact no chance to build some pyramids without this triangle: all 1:21-pyramids!
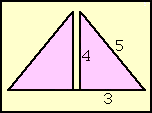The triangle can be found in the pyramid of Chephren. If you (please, children, don't do this at home) saw through that pyramid right in the middle you will see, that both so constructed triangles are perfect 3:4:5-triangles. But this is no mystery at all. As you remember, the Egyptians used length/height-ratios to construct pyramid slopes. Mostly used were 1:22 and 1:21-ratios, one cubit height to 21 or 22 fingers length. If you substitute the cubit with the fingers it consists of, you get for Kephrens pyramid a 28:21-ratio. Divide this by 7, and you get a "3 units length by 4 units height"-ratio. These are the short sides of a holy triangle, so the third side must then be in a "5 units"-ratio in respect to the other sides. Therefore, all pyramids in Egypt constructed in the 1:21-ratio are carrying the 3:4:5-ratio quite naturally.
The holy triangle or its appearence in some pyramids is therefore no sign, that old Egypt knew anything about higher geometry.
Pyramid mysteries