Mit den auf den vorherigen Seiten ermittelten Zahlen werde ich jetzt die konkrete Leistung der Manna-Maschine betrachten. Sollte ich mich an einer Stelle geirrt haben, korrigieren Sie mich bitte!
Ich werde jedes Szenario
jeweils für beide Maschinengrößen (Sassoons Original und das in der heutigen PS adaptierte Modell) berechnen.
Aus der Molekulargewichtstabelle können wir entnehmen, wieviel Wasser und Kohlendioxid benötigt werden. Für spätere Verwendung habe ich auch noch die stündliche Menge angegeben:
| Modell | Biomasse[kg] | Wasser | Wasser/Stunde | CO2 | CO2/Stunde |
|---|---|---|---|---|---|
| 1 (Hungerdiät) | 1145 | 687 kg | 28,62 l | 1679 kg | 69,97 kg |
| 2 (normale Ernährung) | 1418 | 850 kg | 35,45 l | 2080 kg | 86,66 kg |
| 3 (Großfamilie) | 3164 | 1898 kg | 79,1 l | 4640 kg | 193,4 kg |
Interessant: Obwohl ich auch Dale/Sassoons Spardiät betrachte, kommen sie in ihrem Buch auf völlig andere Mengenangaben. Warum? Nun, weil die beiden Autoren klammheimlich und kommentarlos den Kalorienbedarf des "Volks Israel" zusammenkürzen:
"Bei dieser Berechnung wird davon ausgegangen, daß jeden Tag 800 Kilo in Form von Kohlehydraten benötigt wurden"[ 1 ]
Aha, seltsam, bei der ursprünglichen Berechnung des Kalorienbedarfs auf S. 122 ihres Buchs gingen sie noch von 800 Kilogramm Gesamtmasse mit einem Brennwert von 5.5 kCal/Gramm aus, woraus sie hier einfach 800 kg Kohlehydrate mit lediglich 4.1 kCal/g machen. Dadurch haben sie bei gleicher Masse auf einmal erheblich weniger Brennwert. Die Konsequenz daraus? Die armen Israeliten müßten nun mit durchschnittlich 1093 kCal/Person auskommen - statt ihrer ursprünglichen Hungerdiät von schon viel zu wenigen 1260 kCal/Person (zur Erinnerung: für "leichte körperliche Arbeit" wäre bei Dale/Sassoons Familienverband sogar eine Mindesversorgung von 1740 kCal/Person nötig!)
Die beiden Autoren haben also einfach 1/3 notwendiger Produktionsleistung eliminiert - und brauchen plötzlich nur noch 1170 statt 1679 kg CO2 pro Tag. In meinen Augen ist das ein ziemlich windiger Trick - dem noch mehrere folgen werden! Die einzig korrekte Methode ist aber, die Maschinenproduktion Kalorien- und nicht mengenmäßig umzulegen, daher die Diskrepanz zwischen meinen und Dale/Sassoons Werten.
Zur Erzeugung der Glukose, aus der die Pflanzen überwiegend bestehen, wird eine bestimmte Licht-Nutzleistung benötigt. Da die Chloroplasten durch die Trägheit der Photosynthese-Reaktion nur knapp 14% der einfallenden Photonen nutzen können, wird eine größere Licht-Gesamtleistung benötigt. Die Parameter finden Sie in der folgenden Tabelle:
| Modell | Licht-Nutzleistung | Licht-Gesamtleistung |
|---|---|---|
| 1 (Hungerdiät) | 66.3 GigaJoule | 473.6 GigaJoule |
| 2 (normale Ernährung) | 82.1 GigaJoule | 586.4 GigaJoule |
| 3 (Großfamilie) | 183.1 GigaJoule | 1310 GigaJoule |
Bei einer Debatte über die Maschine mit Christian Forrer, der mich in der Anfangsphase dieses Themas freundlicherweise mit den korrekten Sassoon-Daten bestückte, fiel mir ein fataler Verständnisfehler auf, der unter anderem auch Dale/Sassoon unterlaufen sein könnte.
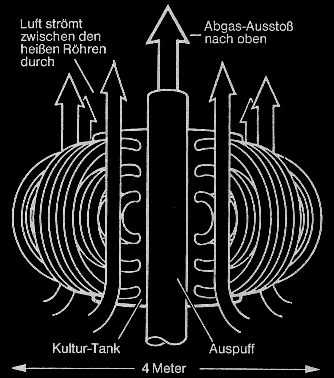
Die Maschine soll eigentlich rein passiv arbeiten, und Wasser sowie Kohlendioxid aus der Luft auskondensieren. Dazu ist natürlich eine Windbewegung notwendig, die feuchte, Kohlendioxidreiche Luft an die Maschine heranführt, und die verbrauchte trockene Luft abtransportiert. Setzt man nun z.B. die Gesamtoberfläche der Austauschröhren für CO2 auf 160 m2 an (den Wert kann man grob aus Dale/Sassoons Skizzen errechnen) wäre also die nötige Windgeschwindigkeit, die zur Heranschaffung "unverbrauchter" Luft notwendig ist, durch "Nötige Menge / Quadratmeter Röhrenoberfläche" zu berechnen.
|
"Der Auspuff war senkrechtstehend ... und sobald er heiß genug war, zeigte er die Wirkung eines Kamins. War erstmal alles heiß genug, würde die Luft alleine schon wegen dieses Effekts durch die Maschine donnern..."[ 3 ]
Schaut man sich die Skizze an ist auch klar, daß oberhalb des "Äquators" der Austauschkugel keine Luft mehr von außen in die Röhren eintreten kann, da diese von der aufwärts gerichteten Luftströmung mitgerissen würde. Denn die irgendwo angesaugte Luft muss auch wieder irgendwohin abströmen.
Was man gelten lassen könnte wäre im Maximalfall eine Einbeziehung der gesamten unteren Hemisphären-Oberfläche. Da die Austauschrohre auf dem Kult-Tank sitzen, ist dies keine Kugel mit 4 Metern Durchmesser, sondern ein Volltorus mit einer Höhe von 2 und einem Durchmesser von 4 Metern. Gemäß des Guldinschen Postulats können wir eine Gesamtoberfläche der Konstruktion zu 39 m2 berechnen, die maximale Nutzfläche läge also bei knapp unter 20 m2. Bei dieser Betrachtung muss man natürlich noch die Bodenplatte des Kulturtanks abrechnen, deren Größe knapp 3 m2 beträgt. Somit bleiben maximal 16.6 m2 an Einströmoberfläche übrig, verglichen zu den 12,56 m2 des Anströmquerschnitts sind das 25% Unterschied. Die Wahrheit dürfte bei Kaminwirkung zwischen den beiden Extremen liegen.
Und, ja, dasselbe gilt auch für die Sonne. Ich kann nicht hingehen und sagen "Die Röhren haben 160 m2 Oberfläche, also kann ich Licht von 160 m2 nutzen"; Auch hier ist die der Sonne zugewandte Querschnittsfläche der Sonne entscheidend, auf den die Lichtleistung fällt. All dies ist, wie sich der aufmerksame Leser gedacht hat, entscheidend für Sein oder Nichtsein der Manna-Maschine...
Interessanterweise flunkern Dale/Sassoon hier ihren Lesern schon etwas vor. Einerseits zeigen sie ihre Strömungsskizze, bestätigen den Kamineffekt - und nennen andererseits Zahlen, die mit ihren Angaben schlicht nicht hinhauen. Denn:
"Als nächstes können wir den CO2-Bedarf von 1170 kg pro Tag beurteilen. Der CO2-Anteil in der Atmosphäre ... beträgt gegenwärtig ... 0.59 Gramm pro Kubikmeter. Bei einer hundertprozentigen Absorptionsfähigkeit benötigte unsere Maschine also 23 Kubikmeter Luft zur Deckung...
Wenn die in Abbildung 14.2 angegebenen Größenverhältnisse stimmen, könnte der darauf beruhende Luftdurchfluß mit der Geschwindigkeit von einem halben Meter pro Sekunde ausreichen, um genug CO2 mit den Röhren in Verbindung zu bringen."[ 4 ]
Nachrechnen... Gut, die 23 Kubikmeter stimmen. Um damit aber auf 0.5 m/s zu kommen, würden sie eine Einströmoberfläche von 46 Quadratmetern benötigen - das ist mehr als die gesamte theoretisch zur Verfügung stehende Fläche von 33.2 Quadratmetern! Diese Angabe ist also ein schlichtes Ding der Unmöglichkeit, selbst wenn im Innern der Maschine ein schwarzes Loch wäre. Umgesetzt auf die reale zur Verfügung stehende Fläche haben benötigen sie eine Windgeschwindigkeit zwischen 1.3 und 1.8 m/s. Mit der echten Produktionsmenge von 1679 kg landen wir übrigens schon bei 32 Kubikmetern pro Sekunde oder 2.6 m/s Strömungsgeschwindigkeit...
Zuerst mal braucht die Manna-Maschine viel Wasser. Selbst bei Dale/Sassoons Hungerdiät 28,62 Liter pro Stunde, bei meiner Drei-Generationen-Familie sogar 79,1 Liter. Das Wasser soll aus Luft auskondensiert werden, die über eine gekühlte Oberfläche geblasen wird, auf der dann das Wasser auskondensiert. Dabei wird die Luft durch den "Mund" der Maschine in den kuppelförmigen Kondensor an der Spitze der Maschine geblasen.
Das Wasser muss irgendwo herkommen. Wenn mich meine (arg eingerostete) Physik nicht ganz verlässt, hat Wasserdampf bei 40C einen Teildampfdruck von 73.7 hpa, also wären bei 100% Luftfeuchte Pi mal Daumen maximal 80 g Wasser pro Kubikmeter Luft enthalten. Nun ist die Wüste Sinai keine tropische Oase, sondern, wie der Name sagt, eine Wüste. Mit Luftfeuchten um 10% oder drunter.
Im Juni 2000 war ich im Zentralsinai. Zeigte mein mitgenommenes Hygrometer in Küstennähe noch um die 30% an, sank der Wert bis zur Mitte unter dem von meinem Messgerät erfassbaren bereich von 5%! Das wären dort nur noch 4 g/Kubikmeter Luft.
Sassoon geht von 4.7 g/m3 Luft aus[ 5 ], den Wert werde ich für die Rechnungen übernehmen. Demnach benötigt die Maschine pro Tag die gesamte Feuchtigkeit aus 146170 m3 (Sassoons Hungermodell) bis 403829 m3 Luft am Tag. Die Differenz zum Buch (102000 Kubikmeter) liegt wieder an der Differenz durch die illegale Mengentransformation durch die Autoren.
Hier nochmal in Tabellenform:
| Familientyp | m3 gesamt | m3 pro Stunde | m3 pro Sekunde |
|---|---|---|---|
| 1 (Hungerdiät) | 146170 | 6090 | 1,69 |
| 2 (normale Ernährung) | 180851 | 7535 | 2,09 |
| 3 (Großfamilie) | 403829 | 16826 | 4,67 |
Die Luft um die Maschine herum muss konstant ausgetauscht werden, damit die bereits entfeuchtete Luft ab- und neue Feuchtluft zugeführt werden kann. Das Einströmen der Luft soll völlig passiv erfolgen, im Prinzip "stanzt" die Mundöffnung ein Loch aus der anströmenden Luft (die durch den Kamineffekt des Auspuffs und der Austauschröhren nach oben befördert wird). Das alles soll gemäß der Autoren bei sanften 1,5 m/s Luftströmung erreichbar sein.
Wesentlich für die Maschine ist daher die Luftschicht in Höhe der "Mundöffnung". Diese wird im Buch etwas seltsam angegeben:
"Vorausgesetzt der Mund (oder Lufteinlass) hatte einen Durchmesser von einem Quadratmeter..."[ 6 ]
Durchmesser in Quadratmeter? Auf den Skizzen im Buch ist der Eintritt rechteckig, mit einer maximalen Breite von einem Meter (gemessen am Durchmesser des Tanks), daher ist wohl eine Breite von einem Meter und eine Fläche von 1/2 m2 gemeint -übertragen auf die kleine Maschine wäre das nur 0,0655 m2 bei der kleinen Maschine. Das bedeutet, daß bei einer Windgeschwindigkeit von 1 m/s (3,6 km/h) in einer Sekunde 0,5 m3 Luft in die große und 0,0655 m3 in die kleine Maschine einströmen können - das wären bei vollständiger Entfeuchtung 2.35 g Wasser pro Sekunde bei der grossen, und schlappe 0,16 g/s bei der kleinen Maschine! Die Berechnung der nötigen Windgeschwindigkeit ist einfach: 2 x Luftdurchsatz bei der Großen, und 15 x Luftdurchsatz bei der kleinen Maschine. Um die benötigte Luftmenge in die Maschinen zu bekommen, sind folgende dauerhafte Windgeschwindigkeiten Vwind um die Maschine herum unabdingbar:
| Modell | Vwind km/h | Vwind m/s | Windstärke/Beaufort |
|---|---|---|---|
| 1 (Hungerdiät) | 13,8 | 3,38 | 3,5 - Schwache Briese |
| 2 (normale Ernährung) | 15 | 4,18 | 3,5 - Schwache-mäßige Briese |
| 3 (Großfamilie) | 33,6 | 9,34 | 5,5 - Frische Briese |
| Modell | Vwind km/h | Vwind m/s | Windstärke/Beaufort |
|---|---|---|---|
| 1 (Hungerdiät) | 97,44 | 27,04 | >10 - schwerer Sturm |
| 2 (normale Ernährung) | 120,56 | 33,44 | >12 - über Orkan |
| 3 (Großfamilie) | 296 | 74,72 | >12 - über Orkan |
Die Kleine Maschine ist hier bereits erledigt, denn diese Geschwindigkeiten können passiv nicht erreicht werden. Die große Maschine ist noch machbar - aber nur wenn man, wie die Autoren ohne jeden Beleg behaupten, die Luft zu 100% entfeuchtet werden kann. Ist das realistisch?
Klare Antwort: nein.
Aus den Zeichnungen der Maschine durch Dale/Sassoon kann man sehen, daß diese innere Kondensorkuppel zwischen 0.36 und einem Meter Durchmesser besitzt, je nachdem ob man von einer 1.8 m oder 5 m hohen Maschine ausgeht. Die Anström-Oberfläche der Halbkugeln liegt demnach zwischen 0.2 und 0.64 m2. Auf dieser gekühlten Oberfläche soll laut Dale/Sasson also zwischen 0.5 und 1.5 Liter Wasser pro Minute kondensieren - in trockener Wüste!!! Weil sie einfach stillschweigend und ohne Angabe von Gründen davon ausgehen, daß eine 100%ige Entfeuchtung realisiert werden kann. "Weil wir von einem Taupunkt von 0° ausgegangen sind" sehe ich zumindest nicht als Erklärung, das ist Technobabble auf das hoffentlich nur sehr leichtgläubige Leser hereinfallen.
Jeder kann dazu einen Versuch hier bei uns durchführen: Salatschüssel in den Kühlschrank, ordentlich durchkühlen lassen, am besten ein Eis-Wasser-Salz-Gemisch hineingeben und nach ein Paar Stunden herausnehmen. Wieviele Liter bekommen Sie in der ersten Minute zusammen? :-) Ich wette, selbst hier in unserer feuchten Luft werden es nur ein paar Mililiter sein. Und auch, ob sich die Kondensationsrate durch Luftumwälzung dramatisch gesteigert wird, lässt sich so testen.
Mein Testergebnis von Freitag, dem 6.8.99: Temperatur 28C, Luftfeuchtigkeit 70%. Versuchsobjekt geriffelte Glas-Salatschüssel, gefüllt mit Eiswasser knapp über 0C, Durchmesser 30 cm, Oberfläche 0.14 m2 = 22-70 % der Maschinenoberfläche, durch einen starken Ventilator angeblasen. Ich sollte also mindestens 115 ml/min für Sassoons Hungermodell, bis 320 ml/min für eine vernünftige Familiengröße erzielen. Gemessen Menge: Weit weniger als 1 ml in 10 Minuten!!!
Mehr ist auch nicht zu erwarten. Schaut man sich z.B. bei unter www.cybercool.de/luftentfeuchter die Leistung moderner Industrie-Luftentfeuchter an, wird einiges klarer. Hochleistungsgeräte können bei 80% Luftfeuchtigkeit pro Stunde aus 220 m3 Luft nur rund 875 Milliliter Wasser gewinnen, aus jedem Kubikmeter also 3.97 Gramm oder 14,7%. Bei 80% Luftfeuchte, anstatt der 14%, von der die Autoren ausgehen. Dies ist wichtig, weil bei sinkendem Dampfdruck der Wirkungsgrad der Maschine sinkt, da das Aufnahmevermögen der Luft für Wasser steigt. Man kann bei Halbierung der Luftfeuchte auch von einer Halbierung des Wirkungsgrads ausgehen. Bei 40% Luftfeuchte läge der Wirkungsgrad daher bei rund 8%, bei 20% im Bereich um 5%. Bei einer Luftfeuchte wie der von Dale/Sassoon propagierten haben moderne Luftentfeuchter praktisch überhaupt keine Chance, Wasser zu entziehen. Die von Dale/Sassoon angegebenen 100% sind daher eine reine Wunschvorstellung. Geht man bei der Manna-Technik von ähnlicher Effizienz wie bei uns heute aus, kann sich jeder die Folgen selbst ausdenken.
Noch ein Zahlenwert: Moderne Luftentfeuchter benötigen bei 80% Luftfeuchte 5280 Kubikmeter Luft pro Tag für 21 Liter Wasser, für Sassoons kalkulierten Bedarf bei Hungerdiät also 334400 m3Luft - fast das Dreifache des Sassoonschen Wertes! In feuchttropischer Umgebung.
Setzen wir generös 10% als Wirkungsgrad an (was dreimal so gut ist wie der Stand moderner Technik), haben wir auch für die große Maschine bereits Windgeschwindigkeiten zwischen 130 und 330 Stundenkilometer - einfach unrealistisch.
Tatsächlich noch schwerwiegender ist die Herkunft des Kohlendioxids. Dale und Sassoon kommen für ihre 800 kg Algen auf einen Bedarf von rund 1170 kg dieses Gases, also genau wie ich auf eine Rate von 1.47 kg pro kg Nutznahrung. Sassoon selbst geht davon aus, dass rund 10% des an den Austauschröhren vorbeiströmenden Kohlendioxids genutzt werden kann, ich übernehme diesen Wert.
Halt, Moment nur in ihrem Artikel nennen sie genaue Werte - in ihrem Buch drücken sie sich um genaue Angaben! Wareum werden wir gleich sehen...
CO
So stand es bis Herbst 2006 auf dieser Seite. Im November 2006 begann jedoch der Autor Dieter Bremer, der eine funktionierende Manna-Maschine für seine völlig abstrusen Thesen benötigt, an dieser Darstellung herumzukritteln. Völlig falsch sei das, um Größenordnungen daneben, und daher inakzeptabel.
In der Tat habe ich hier vereinfachend für die Überschlagsrechnung vorausgesetzt, daß die Dichte der Luft und von CO2 identisch sind - was nicht stimmt. CO2 ist um den Faktor 1.5 schwerer als Luft, ein Volumen% entspricht also 1.5 Gewichts%. Mit den Werten von oben gerechnet wären also 0,63 g statt 0,42 g/m3 Kohlendioxid in der Luft. Zwar nicht um Größenordnungen daneben, aber doch merklich.
Lustigerweise gehen Dale/Sassoon von 0.59 g/m3 aus, 0,09 g mehr als miene Überschlagsrechnung. Allerdings waren meine damaligen Abschätzungen eh eher daneben, da ich z.B. die Luftdichte viel zu hoch angesetzt habe. Die 1.4 kg pro Kubikmeter entspricht Luft bei -30°C, warme Luft ist erheblich dünner. Und da sich Kohlendioxid in diesem Druck- und Temperaturbereich ebenso wie die Restbestandteile der Luft wie ein ideales Gas verhält, ist es im gleichen Maße betroffen.
Die Dichte von Luft bei +30°C beträgt nur 1,164 kg pro Kubikmeter[ 7 ], ist also 17% leichter als in meiner Berechnung oben. Aufs Kohlendioxid zurückgerechnet entspricht das dann 0,52 g/m3. Da ich eh mit 0,5 g/m3 gerechnet habe, entspräche das einer Abweichung von 4%. Leider war Herr Bremer nicht in der Lage, das zu verstehen, und krakeelte weiterhin etwas von unerträglichen Fehlern und Uneinsichtigkeit.
Nun, wenn wir schon mal am Korrigieren sind, können wir auch gleich ein paar weitere frühere Abschätzungen konkretisieren. Ich hatte für meine damaligen Kalkulationen unseren heutigen CO2-Anteil verwendet, der durch die Verwendung fossiler Brennstoffe viel höher ist als der zu Exodus-Zeiten. In vielen Tabellen und Diagrammen fand ich, daß noch um das Jahr 800 n. Chr. der Anteil um 270 PPM lag[ 8 ][ 9 ], und in den davorliegenden Jahrtausenden sogar noch deutlich darunter lag.
Rechne ich nur mit den fürs Jahr 800 nachgewiesenen 0,027%, komme ich auf einen Kohlendioxid-Anteil von 0,47 g/m3, und der liegt schon deutlich unter der von mir in meinen alten Berechnungen verwendeten Berechnungsschwelle von 0,5 g/m3.
Spaßigerweise betuppen Dale/Sassoon ihre Leser hier, indem sie schreiben:
"Der CO2-Anteil in der Atmosphäre weist keine großen Schwankungen auf und beträgt gegenwärtig etwa drei Zehntausendstel oder 0,59 Gramm pro Kubikmeter."[ 10 ]
Das stimmt natürlich nicht mit der Realität überein und ist entweder schlampig recherchiert, oder (wie man aus den anderen "Fehlern" schließen könnte) eine bewusste Täuschung.
Besagter Autor Dieter Bremer, nach eigenen Angaben gelernter Chemotechniker, verstand das merkwürdigerweise nicht und führte lediglich gebetsmühlenartig Dale/Sassoons Wert von 0,59 g/m3 an, mit dem alles wunderbar funktioniere (obwohl es nur 20% mehr Kohlendioxid ist). Aber wie kommen die Autoren auf diesen Wert? Ganz einfach, sie verwenden einfach 300 PPM Kohlendioxid, und die Dichte von CO2 unter Normalbedingungen. Das sind 1013 hPa Druck - und 0°C Temperatur! Das ist ein für die Wüste Sinai ziemlich ungewöhnlicher Wert, als ich im Jahr 2000 dort war, war es auch in der tiefsten Nacht brühwarm. Lediglich im tiefsten Winter kann es mal vorkommen, daß dort in der Nacht leichter Nachtfrost auftritt, Dale/Sassoons "Normalbedingungen" sind also keine Normalbedingungen für den Sinai. Außer wir verpflanzen den Exodus nach Grönland...
Hier haben wir die Autoren also erneut beim Schummeln erwischt - man sollte mal den akkumulativen Wert ihrer Schummelei zusammenrechnen, denn immerhin haben sie sich hier schlappe 25% mehr Kohlendioxid "beschafft" 1/3 hier, 25% dort, 40% hier... da läppert sich was zusammen.
Kontrollieren wir mal meinen Verdacht.Bei 300 PPM und einer Normaldichte von 1,977 kg/m[ 11 ] erhalten wir in der Tat 0,593 g/m3. Wie sich CO2 bei höheren Temperaturen verhält können wir ausrechnen, indem wir die Formel für ideale Gase verwenden. Also Dichte = (Druck in kPa x Molmasse) / (Gaskonstante 8,314 x absolute Temperatur).
Da diese Formel nur ungefähr funktioniert, kann man nicht einfach die Molmasse 44 für CO2 eingeben, da dann eine Dichte von 2 kg/m3 bei Normalbedingung herauskäme, wir müssen erstmal die einsetzbare Molmasse durch Auflösung bei Normalbedingung ausrechnen. Es ergibt sich 44,31. Setze ich diesen Wert in die obige Gleichung ein und wähle eine Temperatur von 30°C ergibt sich eine Dichte für CO2 von 1,781 kg/m3. 3 Liter davon (entspricht 0,03 vol% Anteil an der Luft) haben also eine Masse von 0,53 g/m3, 1/100 Gramm oder weniger als 2% mehr als bei meiner verwendeten Methode. Mit den historisch korrekten CO2-Werten landet man bei 0,48 g/m3, also erneut unter meiner Berechnungsbasis von 0,5g/m3 und schlappe 20% weg von Dale/Sassoons Fantasiewerten..
An meinen folgenden Berechnungen ändert das alles also überhaupt nichts!
Also geht's nun unverändert weiter im Text:
Der Austausch soll laut Sassoon passiv über halbdurchlässige Schläuche geschehen, setzt also erneut Windbewegung voraus. Nach Sassoons eigenen Angaben hat die Maschine einen größten Durchmesser von 4 Metern, das entspricht, wie auf der vorherigen Seite zu lesen, einem Anströmquerschnitt von 12.5 m2 für die große, und 1.6 m2 für die kleine Maschine. Interessanterweise ergeben sich hier bereits mit den Originalwerten von Dale/Sassoon unmögliche Werte. Zur Erinnerung: Sie benötigen 1170 kg CO2 für ihre Hungerdiät, gehen selbst von 10% Wirkungsgrad aus - und benötigen daher mit den korrekten CO2-Werten über 23 Mio m3 Luft am Tag! Das wäre für die große Maschine eine dauerhafte Windgeschwindigkeit von 77 Stundenkilometer - schwerer Sturm!
Diese Hungerdiät basiert aber, wie ich schon mehrfach erwähnte, auf kreativ zusammengestrichenen Produktionsdaten. Mit korrekten Werten (siehe Tabelle 1) ergeben sich diese Werte:
| Modell | Luft[Mio. m3 | Vwind km/h | Vwind m/s | Windstärke/Beaufort |
|---|---|---|---|---|
| 1 (Hungerdiät) | 33,58 | 111,93 | 31,09 | 12, schwerer Orkan |
| 2 (normale Ernährung) | 41,60 | 138,66 | 46,22 | >12, über Orkan |
| 3 (Großfamilie) | 92,80 | 309,33 | 103,11 | >12, über Orkan |
Selbst wenn die Luft "magisch" von der Maschine angezogen wird (und dann z.B. nach oben durch "Thermik" abgeblasen wird) ändert sich nicht viel, da die Fläche gerade mal um 25% steigt. Es blieben immer noch Geschwindigkeiten zwischen 80 km/h (Windstärke 7, sehr steifer Wind) und 170 km/h (Windstärke 12+, schwerer Orkan) übrig. Und oben, wo die Luft per "Kaminwirkung" abfließen soll, müssten trotzdem die oben in der Tabelle aufgeführten Windgeschwindigkeiten auftreten. Wie mann es dreht oder wendet, am katastrophalen Ergebnis ändert sich überhaupt nichts.
Die Maschine soll, das möchte ich nochmal betonen, laut Bibel versteckt in einem GESCHLOSSENEN Stiftszelt gestanden haben - die Autoren haben aber immerhin gemerkt, daß das nicht klappt und daher allerlei lustige Ideen drumherum gestrickt. Aber gehen wir mal von der Bibel aus: Können Sie sich vorstellen, wie ein solches Zelt gebaut gewesen sein müßte? :-D
Um es deutlich zu machen: Meine Berechnung setzt voraus, daß die Austauschröhren es wirklich schaffen, beim Durchfluß der Luft insgesamt 10% des CO2 zu entziehen! Ein Wert der wahrscheinlich noch viel zu hoch ist.
Selbst bei 100% Wirkungsgrad - der Luft würde sämtliches CO2 entzogen - läge die ständig nötige Anströmgeschwindigkeit zwischen Windstärke 4 und 8 (stürmischer Wind).
Halt, Moment, die Maschine soll ja nur 6 Tage die Woche arbeiten, und in der Zeit Überschuss für den Sabbat produzieren - das erhöht den nötigen Luftdurchsatz um weitere 15%. Tja, das wars wohl endgültig.
Letzter Punkt ist die Energiedichte. Wir haben oben gesehen, daß aufgrund des geringen Wirkungsgrades der Photosynthese zwischen 473 und 1310 GJ pro Tag Lichtleistung benötigt werden. Vorausgesetzt, es wird exakt Licht der benötigten Wellenlänge eingestrahlt, wie es Dale/Sassoon per Laser machen wollten.
Pro Sekunde benötigt man also die Lichtleistung von knapp 5.4 bis 15.2 MJ. Nun ist 1 J/s aber ein Watt - man braucht also eine Dauer-Lichtleistung von 5.4 bis 15.2 Megawatt. Ups, bereits die Lichtleistung liegt um den Faktor 10 höher als das was Dale/Sassoon als maximale ELEKTRISCHE Leistung der Maschine angeben!!! Dumm gelaufen... Schlimmer: Laser können aus physikalischen Gründen nur mit relativ geringer Wirkleistung arbeiten, wir liegen momentan bei 10% und drunter. Selbst bei 30% Wirkungsgrad müßte die elektrische Leistung von mehr als 15 Megawatt reingeschoben werden - bei Dale/Sassoons Kleinfamilie auf Hungerdiät!!
Aber Rettung naht! Am Tag kann ja die Sonne helfen. Denn immerhin stehen ja 160 Quadratmeter durchsichtige Röhren als Empfänger für Sonnenlicht zur Verfügung.
Kaum. Wie schon oben beschrieben, kann man ausschließlich die Energie nutzen, die auf den der Sonne zugewandten Querschnitt der Maschine fällt. Die Anzahl oder Dichte der Röhren beeinflusst lediglich den Wirkungsgrad, mit dem das auf dieser Fläche zur verfügung stehende Potential genutzt wird! Bei einer Brutto-Lichtleistung von 1 kw/m2 oder einer genutzten Nettoleistung von 14 kj/s/m2 und 7 m2 beleuchteter Querschnittsfläche kann die Sonne gerade mal 1.8% des Hungerdiät-Energieverbrauchs während der Stunden mit Tageslicht decken - oder 0.9% des Tagesbedarfs.
All dies ist recht vernichtend und vor allen Dingen auch noch überprüfbar. Wie um alles in der Welt Sassoon und Dale auf ihre Konstruktionsschätzungen gekommen sind, ist mir schleierhaft. Insbesondere der reine Energiebedarf, Windgeschwindigkeit und das CO2-Problem hätten sie ihr Modell doch überdenken lassen müssen. Außer sie liefen in die oben erwähnte Spezialfalle.
Eigentlich wollte ich noch auf andere Probleme eingehen:
Erschreckend: Die These wird seit nunmehr 25 Jahren von verschiedenen Bestsellerautoren durch die Publikationen getrieben, ohne die von Sassoon/Dale vorgelegten Zahlen und Daten nachzuprüfen! Obwohl sie, da muss man sie wirklich loben, ihre Konstruktion so transparent dargelegt haben, daß man sie überprüfen kann. In der PS ist das keine Selbstverständlichkeit!
Speziell die in der PS wegen ihrer Transportabilität bevorzugte (und wie wir gesehen haben von Sassoon korrekt abgelehnte) kleine Maschine ist ein katastrophaler Reinfall.
Diese Berechnungen präsentierte ich im Juni 1999 auf dem schon angesprochenen Diskussionsforum der A.A.S. dem leider zu früh verstorbenen Dr. Johannes Fiebag, Autor zweier Bücher über die Hintergründe des Grals, den nicht nur er für die Manna-Maschine hält. Dieser war recht verblüfft über die Resultate, gab aber zu, den Werten von Sassoon vertraut zu haben, da sie eben mit detaillierter Ausführlichkeit dargelegt wurden und daher glaubhaft wirkten. Zudem gab er zu (auch nicht oft anzutreffen), nicht über ausreichende Kenntnisse auf dem Gebiet zu verfügen um dies zu verifizieren. Er versprach allerdings, meine Berechnungen umgehend an Sassoon, mit dem er in engerem Kontakt steht, weiterzuleiten. Ich versprach im Gegenzug, Sassoons Entgegnungen auf meiner Homepage zu veröffentlichen. Die recht unbefriedigende Antwort finden Sie auf der folgenden Seite.
| Anmerkungen: | ||
| [1] |
Dale/Sassoon; Die Manna-Maschine, S. 273 |
|
| [2] |
ibid., S. 275 |
|
| [3] |
ibid., S. 277 |
|
| [4] |
ibid., S. 274 |
|
| [5] |
ibid. |
|
| [6] |
ibid. S. 277 |
|
| [7] |
Wikipedia: Luft |
|
| [8] |
Uni Bremen, Atmosphäre CO2 during the last 60000 years |
|
| [9] |
Dale, Sassoon S. 274 |
|
| [10] |
CO2 seit 950 n. Chr. |
|
| [11] |
Wikipedia: Dichte gasförmiger Stoffe |
|
  | Zurück: Produktionsraten | Weiter: Sassoons Kommentar |   |