Ein Hauptelement in Bauvals Begründung nehmen allerdings "optische Übereinstimmungen" ein. Das beginnt schon bei den Pyramidengrößen:
"Die Anlage der drei Pyramiden entspricht nicht nur der Lage der drei Sterne mit erstaunlicher Präzision, sondern die Leuchtkraft der Sterne, die sich aus ihrer Größe ergibt, entspricht auch der Größe der einzelnen Pyramiden."[ 1 ]
Dummerweise sagt Bauval nicht, was er mit Größe meint. Volumen, Oberfläche oder Höhe? "Höhe" wäre die natürliche Annahme, aber untersuchen wir erstmal die beiden anderen Alternativen:
Der optische Eindruck der Sterne ist "zwei gleich helle und ein etwas dunklerer". Würde man aber die Volumenverhältnisse der Pyramiden als Vergleich heranziehen, müßten die beiden helleren Sterne aber rund zehn mal so hell sein wie der dritte Stern, da das Volumen der dritten Pyramide gerade mal 10% des der anderen beträgt. Das widerspricht klar dem Eindruck am Himmel, das Volumen scheidet als Größendefinition also aus.
Betrachtet man die Oberflächenverhältnisse, so müßten die helleren Sterne noch fünfmal so hell sein, nimmt man die Verhältnisse der Basisquadrate noch immer rund viermal. Daher bleibt nur die Höhe als möglicher Vergleich.
Bauval gibt nirgendwo exakte Daten an, er betont nur, daß die Pyramiden genau die Helligkeitsunterschiede wiedergeben. Das bedeutet, daß der Stern der Mykerinospyramide rund 50% der Helligkeit der beiden anderen Sterne besitzen sollte, und daß die beiden anderen Sterne praktisch gleich hell sein müßten.
Das widerspricht aber eklatant astronomischen Tabellenwerken, wie dem Yale catalogue of bright stars (3rd Edition)oder dem Katalog meines Astronomieprogramms Redshift:
| Stern | Pyramide | mag Yale | mag Redshift |
|---|---|---|---|
| Zeta ORI | Cheops | 2.05 | 2.00 |
| Epsilon ORI | Chefren | 1.70 | 1.70 |
| Delta ORI | Mykerinos | 2.2 - 2.7 (var) | 2.50 |
Der 'Mykerinos'-Stern ist variabel, seine Helligkeit schwankt zwischen 2.2 und 2.7.
Sternhelligkeiten werden in der Einheit 'mag' ausgedrückt, die bei mit bloßem Auge sichtbaren Sternen Werte zwischen 5 und -1 annehmen kann. Dabei entsprechen 5 mag einem gerade noch mit dem bloßen Auge sichtbaren Stern, -1 mag erreicht dagegen der hellste sichtbare Stern am Himmel, Sirius. Die Sternhelligkeiten entstammen einer uralten, dem menschlichen Auge angepaßten Skala, die schon die arabischen Astronomen verwendeten. Diese übernahmen sie wahrscheinlich von den Babyloniern. Der Helligkeitsunterschied einer Größenklasse wurde damals so gewählt, daß das menschliche Auge den Unterschied von 1 mag wie eine Verdoppelung oder Halbierung der Helligkeit wahrnimmt.
Unser Auge funktioniert aber nicht linear, das bedeutet, daß die echte gemessene Leuchtkraft eines Sterns von unserem visuellen Eindruck abweicht! Es handelt sich um eine logarithmische Funktion.
Mit bloßem Auge können von erfahrenen Himmelsbeobachtern (zu denen man Priester einer Sternreligion wohl zählen dürfte) Sternhelligkeiten bereits auf 0.2 mag genau bestimmt werden, noch genauer hingegen ist die Abschätzung von Helligkeitsverhältnissen nebeneinander liegender Sterne, wo selbst 0,05 mag keine Besonderheit darstellen (lange bevor elektronische Messinstrumente in Gebrauch waren, setzte man polierte Silberspiegel ein um Sterne zum Vergleich ins Auge des Beobachters spiegeln zu können). Man braucht daher keinerlei komplizierte Messinstrumente, und wenn die Ägypter die Helligkeitsverhältnisse hätten bestimmen wollen, so hätten sie dies auch mit einer Abweichung von wenigen % geschafft.
Der Cheops-Stern ist, wie Sie der Tabelle entnehmen können, in Wirklichkeit schon 30-35% lichtschwächer als der Chefren-Stern und der Mykerinos-Stern wäre im Mittel 50% schwächer als der Cheops-Stern, und 70-80% lichtschwächer als der Chephren-Stern. Man würde also erwarten, eine hohe Pyramide in der Mitte und 2 wesentlich niedrigere Bauten rechts und links davon zu finden, die Cheopspyramide dürfte dabei nicht höher sein als die Knickpyramide in Dahschur. Das widerspricht aber völlig dem Anblick zweier fast gleich hoher Bauten und einer im Vergleich dazu zwergenhaften Mykerinospyramide. Setzt man die Chefrenpyramide mit ihren 143 Metern als Maßstab, sollten die Pyramiden die folgenden Höhen aufweisen:
| Pyramide | Sollhöhe | Wahre Höhe | Fehler |
|---|---|---|---|
| Cheops | 93 - 100 m | 146,6 m | 46 - 57% |
| Mykerinos | 46 - 50 m | 66,5 m | 33 - 45% |
Die Abweichungen zwischen Sternhelligkeiten und Pyramidenhöhen sind meines Erachtens viel zu hoch für eine Korrelation. Fast 60% Fehler bei der Größe der Cheopspyramide - das ist ein dickes Ding. Eindeutig erkennbar: Die Pyramiden geben alles andere als die wahrnehmbaren Helligkeitsverhältnisse der Sterne wieder, der Punkt ist damit eindeutig FALSCH!
In letzter Zeit wurde ich auf andere Tabellenwerke aufmerksam gemacht, in denen etwas andere Angaben zur Sternhelligkeit zu finden sind. Sie geben für den mittleren Stern Helligkeiten zwischen 1.6 und 1.7 an, für den "Cheops"-Stern welche zwischen 1.8 und 2.0. Ich werde dem nachgehen, an der Tatsache des hellsten mittleren Sterns ändert sich dadurch allerdings nichts.
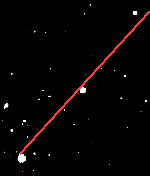
Die Mykerinos-Pyramide wurde mit einer deutlich sichtbaren Abweichung von der Diagonale der beiden anderen Pyramiden gebaut. Laut Bauval ist das ein bewusster Akt, um die gleichgerichtete Abweichung des dritten Oriongürtel-Sterns darzustellen:
"Warum war die kleinste [Pyramide, Anm. FD] nach Osten versetzt? Die Antwort lag auf der Hand: Diese "Anomalien" waren Bestandteil eines Gesamtplans, dessen Umsetzung für den Bau der dritten Pyramide bestimmte Beschränkungen vorsah."[ 2 ]

|
|
Bauval behauptet also, daß die Mykerinos-Pyramide "versetzt" sei. Die Frage ist jetzt, was bedeutet "versetzt"? Legt man drei Münzen, zum Beispiel 2 Zehnpfennig- und ein Einpfennig-Stück an ein Lineal an, ist dann das Einpfennigstück versetzt? Sicher nicht, nur der Mittelpunkt weicht von einer gemeinsamen Linie ab da es eben kleiner ist. Von "versetzt" würde man sprechen, wenn die Anlegekante abweicht.
|
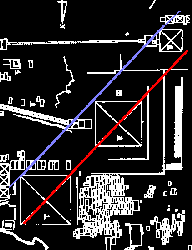
Schon vorher haben wir uns die sogenannte "Giza-Diagonale" angesehen. Die Südostecken aller drei großen Pyramiden liegen, zusammen mit dem Mittelpunkt der ersten Satellitenpyramide von Mykerinos und der ersten des Cheops sowie einer geheimnisvollen Struktur namens "Mauerblock" bis auf wenige Meter Abweichung direkt auf einer Linie, die ins Zentrum der alten Reichshauptstadt zeigte.
Wir haben also eine Situation wie bei den Münzen des Lineals vor uns, bei der der Mittelpunkt der kleinsten Münze von der Linie abweicht, nicht aber die Kante mit der ich sie am Lineal angelegt habe. Ein echter Versatz wie ihn die Sterne deutlich zeigen, liegt nicht vor!
Es gibt noch eine zweite Diagonale: zieht man eine Linie durch den Mittelpunkt der beiden großen Pyramiden, und verlängert diese, berührt diese fast die Nordwestkante der Mykerinospyramide.
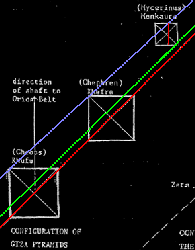
Aber Moment, das hatte ich doch anders in Erinnerung. Ich konnte mich an eine Fernsehsendung erinnern in der ein konkreter Versatz gezeigt wurde. Und in seinem Buch philosophiert Bauvals einige Seiten über diese Abweichung der Mykerinos-Pyramide. Dabei meint er eine echte Abweichung, und hat dazu auch ein Bild: Seine Tafel 12. Legt man ein Lineal an, so weicht die Südost-Kante seiner eingezeichneten Pyramide tatsächlich minimal ab. Leider ist das briefmarkengroße Bildchen nicht geeignet für genauere Messungen, aber bereits 1989 schrieb er einen Aufsatz für Discussions in Egyptology, No. 13. Seine Fig. 2 ist das wonach ich suchte...
|
|
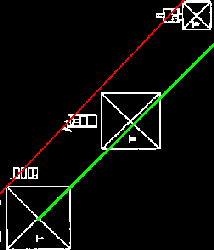
Stimmt, die Situation auf der Skizze ist etwas anders. Die Diagonale stößt durch die Mykerinospyramide hindurch, und tritt auf der Südseite sogar noch jenseits des Pyramidenmittelpunkts aus. Und die Mittelpunktsdiagonale kommt noch nichtmal in die Nähe der Pyramidenkante. Die Ursache findet man, wenn man einmal die DE-Skizze mit anderen Plänen vergleicht: Bauval verwendet für seine Skizze einen etwas anderen Neigungswinkel zwischen Cheops- und Chephrenpyramide, einen flacheren. So erreicht er durch wenige Meter Versatz der Chephrenpyramide eine vermeintlich große Abweichung bei Mykerinos!
Bild 15 zeigt daher die aus Bauvals DE-Skizze gewonnene Neigung übertragen auf den anderen Plan - eindeutig, damit wird die vorgefundene Abweichung erklärbar! Das kann noch weniger Zufall sein als die verbogenen Gantenbrink-Werte und ist in meinen Augen ziemlich dreist.
Dadurch daß die drei Pyramiden auf einer Linie liegen erhält man übrigens erst diesen großartigen "Neun-Pyramiden-Blick", bei dem die Cheops(hinten)- und Mykerinospyramide fast gleichgroß wirken...

Auch dieses Indiz ist also FALSCH!

|

|
Bauvals stärkstes Argument ist aber die Deckung zwischen den Pyramiden und den Sternen, die stets mit den beiden obigen Motiven demonstriert. Was mir aber bereits beim ersten Lesen vom "Oriongeheimnis" auffiel, ist das verwendete miserable Foto des Oriongürtels. Dieses Bild fand ich sogar in einem Buch über die Geschichte der Astrofotografie, es handelt sich um eine der ersten Aufnahmen dieser Himmelsregion durch ein Fernrohr.
Das Bild ist durch die noch primitive Fototechnik völlig überstrahlt und überbelichtet, daher fragte ich mich jahrelang, warum keine aktuellen Fotos verwendet wird, und selbst in neuesten Fernsehproduktionen wie einer kürzlich auf Discovery gesendeten von 1999 noch der alten "Schinken" herhalten muss. Durch ein wenig Überlegung kommt man allerdings darauf. Das Uralt-Foto sorgt nämlich dafür, daß die Sterne ungefähr auf Pyramidengröße aufgeschmiert werden, und somit ein Entfernungs/Größenverhältnisse ähnlich wie in Giza darstellen. Zudem ist der Mittelpunkt der Sterne nicht mehr eindeutig feststellbar, sodaß Abweichungen kaschiert werden können. Es wird ein "gleichartiger Eindruck" suggeriert.



Man sollte daher ein moderneres Orionfoto wie oben verwenden. Siehe da, der optische Eindruck unterscheidet sich erheblich. Statt dreier Riesenkreise, die sich von der Größe her mit den Pyramiden decken, hat man es mit drei sehr weit auseinanderliegenden Punkten zu tun. Auch wenn die Deckung weit besser ist als ich vermutet hätte, entspricht der optische Eindruck des Oriongürtels in keinster Weise dem Eindruck der Pyramiden auf dem Boden. Dazu hätte man drei steile und im Vergleich zu ihrer Fläche weit auseinanderliegende Anlagen benötigt, wie von der Art des Sonnenheiligtums in Abu Gurob. Noch mehr: Es gibt ja nicht nur die drei großen Pyramiden in Giza, sondern noch 6 Satellitenpyramiden, die mit über 30 Metern doch recht erhebliche Höhen erzielen. Durch meine Projektion einer aktuellen Orion-Fotographie mit den Pyramiden erkennt man: Es gibt keine Entsprechungen am Himmel. Warum, wenn alle Pyramiden den Sternen zugeordnet werden sollen? Denn Sterne hätte es, siehe Photo, genug gegeben!

Auch die Abweichung des "Mykerinos"-Sterns im Oriongürtel ist zu klein. Sie ist vom Boden aus praktisch nicht sichtbar. Oder können Sie auf dem obigen Foto erkennen, daß die kleinste Pyramide nicht auf einer Linie mit den anderen beiden steht?


Die Abweichung der Mykerinospyramide von der Diagonalen ist aber vom Boden aus (und das ist die Betrachtungsweise der Baumeister) schlicht nicht sichtbar.
Um sie definitiv zu erkennen, muss. man gut 2-3 Kilometer südöstlich in die Wüste wandern, auf die kleine Erhebung des "Nine Pyramid View", und von da noch ein gutes Stück nach Westen den Hügelkamm entlang. Um einen ähnlich deutlichen Effekt zu liefern wie der Orion-Gürtel, müßte die Mykerinos-Pyramide um mindestens 200 Meter von der Diagonale der Cheops/Chefren-Pyramide abweichen. Und nicht 30 Meter wie in der Realität.
| Anmerkungen: | |
| [1] | Bauval/Gilbert S. 145 |
| [2] | ibd. S. 131 |
  | Zurück: Die Schächte | Weiter: Der Anblick 2 |   |